Circuiti in continua con l'amplificatore operazionale ideale

 Vengono qui di seguito rappresentati alcuni circuiti fondamentali in continua (a ingresso costante) che fanno uso dell'amplificatore operazionale ideale e del suo guadagno infinito, dimostrando che l'uscita non dipende dal guadagno dell'operazionale stesso, ma dal circuito connesso tra l'uscita e i suoi terminali. Sono presenti in questa trattazione l'amplificatore invertente e non invertente, il sommatore analogico, l'amplificatore differenziale e gli amplificatori logaritmico e anti-logaritmico.

Amplificatore non invertente

Il circuito è composto da un operazionale ideale e una coppia di resistenze di valore arbitrario, R1 e R2. Il circuito è mostrato in figura 1: 

Figura 1: amplificatore non invertente.

Le equazioni che regolano il circuito sono le seguenti:

la differenza tra i due valori di ingresso fornisce, ovviamente, la tensione differenziale.

Utilizzando il principio del corto circuito virtuale, secondo cui il guadagno infinito dell'operazionale ideale provocherebbe una tensione differenziale nulla, 

Il risultato ottenuto è che l'uscita è maggiore dell'ingresso del rapporto tra le resistenze.
La relazione è valida fino a quando l'uscita non arriva al valore di saturazione, negativa o positiva.

I valori dell'ingresso per cui l'uscita è pari alla saturazione positiva vale

La caratteristica ingresso-uscita è mostrata in figura 2.

Figura 2: caratteristica statica ingresso-uscita.

Amplificatore invertente

La configurazione circuitale è simile a quella dell'amplificatore non invertente, con la differenza che il terminale non invertente è connesso a massa e l'ingresso è posto prima del resistore che collega il terminale invertente, come mostrato in figura 3.

Figura 3: amplificatore invertente.

Il circuito è governato dalle seguenti leggi:

il calcolo della tensione sul nodo del morsetto non invertente viene fatto a partire dal bilancio delle correnti al nodo stesso, tenendo conto che la corrente entrante nell'operazionale è nulla.

Il terminale non invertente è collegato a massa, per cui la sua tensione è pari a zero. Allora, per il principio del cortocircuito virtuale, le tensioni di ingresso di eguagliano:

Il risultato in regione di alto guadagno è una tensione uscente pari all'opposto dell'ingresso, moltiplicato per un guadagno uguale al rapporto tra le due resistenze. Il momento in cui l'uscita satura positivamente si verifica quando l'ingresso ha valore:

Proprio per definizione di amplificatore invertente, l'uscita satura positivamente al crescere dei valori negativi della tensione d'ingresso. Al contrario per la saturazione negativa. La caratteristica statica è mostrata in figura 4:

Figura 4: caratteristica dell'operazionale invertente.

Sommatore analogico invertente

Il circuito è realizzato come un amplificatore invertente, con la presenza di più ingressi collegati tramite resistore al terminale invertente. Il terminale non invertente è sempre collegato a massa (figura 5).

Figura 5: sommatore analogico.

L'analisi del circuito può essere fatta con il principio della sovrapposizione degli effetti: l'uscita può essere ottenuta calcolando l'effetto dei due ingressi separatamente e sommando i contributi tenendo valida l'ipotesi del cortocircuito virtuale.

Ponendo l'ingresso V2 a zero, non avrà alcun effetto, poiché il resistore R2 ha una differenza di potenziale nulla (i terminali di ingresso sono allo stesso potenziale, zero). Lo schema circuitale è mostrato in figura 6. 

Figura 6: sommatore con ingresso V2 nullo.

Dal circuito in figura 6, poiché la resistenza R2 non ha alcun effetto, è come se non ci fosse. è possibile riconoscere un amplificatore invertente, la cui uscita vale:

Procedendo allo stesso modo, ma collegando V1 a massa, il resistore R1 non ha alcun effetto sul circuito (figura 7)

Figura 7: sommatore con ingresso V1 nullo.

Dal circuito in figura 7, si riconosce ancora un amplificatore invertente, la cui uscita è:

Infine, l'uscita è ottenibile sommando i due contributi:

Nel caso generale, l'uscita di un sommatore analogico con n ingressi e stessa resistenza di riferimento RF vale:

Amplificatore differenziale

il circuito amplificatore differenziale è, in linea teorica, l'opposto del sommatore analogico. L'uscita deve essere il segnale differenza tra due segnali in ingresso. Il circuito è mostrato in figura 8.

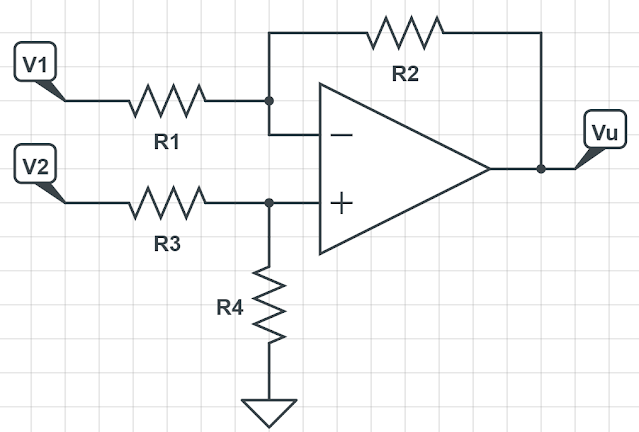Figura 8: amplificatore differenziale.

Non è necessario il principio di sovrapposizione degli effetti, in quanto la tensione sul terminale invertente è ottenibile allo stesso modo dell'amp. invertente, mentre la tensione sul morsetto non invertente è un semplice partitore resistivo con resistenze R3 e R4.

Le relazioni sono dunque:

L'ipotesi di cortocircuito virtuale porta all'uguaglianza dei due valori di tensione appena ottenuti.

Il buon dimensionamento dei resistori prevederebbe che, per una differenza più "pulita", ossia con meno termini resistivi, si impone R1=R4 e R2=R3:

La positività o negatività della tensione di uscita, ovviamente, dipende dall'ampiezza di tensione dei due segnali. Se V2 è maggiore di V1, allora l'uscita è positiva. Viceversa, l'uscita è negativa.

Amplificatore logaritmico

Il circuito logaritmico sostituisce la resistenza connessa tra uscita e morsetto non invertente con un diodo, descritto dalla classica funzione I-V di tipo esponenziale. Il circuito è mostrato in figura 9.

Figura 9: amplificatore logaritmico.

L'analisi parte dal bilancio delle correnti al nodo terminale invertente, considerando sempre nulle le correnti entranti nell'operazionale.

ricavare la tensione al terminale invertente sarebbe complicato e richiederebbe approssimazioni. Si impone quindi la condizione di cortocircuito virtuale, essendo il terminale non invertente a massa:

Come previsto, la tensione di uscita è il logaritmo (opposto) del segnale di ingresso. La caratteristica statica ingresso-uscita è mostrata nel grafico in figura 10: 

Figura 10: caratteristica dell'amplificatore logaritmico.

Al crescere dell'ingresso, la tensione di uscita è sempre negativa.

Il valore di tensione Vi = -RIS è un asintoto verticale della funzione: valori di tensione inferiori a questo non sono matematicamente accettabili.

Amplificatore anti-logaritmico (esponenziale)

Il circuito anti-logaritmico è l'inverso del circuito logaritmico. Il diodo e la resistenza si scambiano di posizione, così che il primo è direttamente collegato all'ingresso. Il terminale non invertente rimane collegato a massa. Il circuito è mostrato in figura 11.

Figura 11: amplificatore anti-logaritmico.

Ora l'equazione delle correnti al nodo del terminale invertente diviene:

passando ancora una volta all'ipotesi di cortocircuito virtuale, eguagliamo la tensione al terminale non invertente alla tensione sul terminale invertente.

Come prevedibile, il risultato all'uscita è l'esponenziale negativo del segnale di ingresso. Il grafico in figura 12 mostra l'andamento dell'uscita al variare della tensione in ingresso.

Figura 12: caratteristica dell'amplificatore esponenziale.

Per le proprietà della funzione esponenziale, al crescere di tensioni negative, l'uscita tende sempre di più verso il valore RIS, prodotto tra resistenza e corrente di saturazione inversa del diodo.