Funzione di trasferimento armonica dei sistemi lineari - poli e zeri

-

 Analizzare un circuito lineare nel dominio delle frequenze consente di ricavare una funzione che descrive l’operato del sistema in relazione ai suoi componenti principali: si tratta della funzione di trasferimento. 

Dato uno stimolo in ingresso e valutata l’uscita, la funzione di trasferimento può essere calcolata secondo alcuni rapporti:

  • Rapporto tra la tensione in uscita e la tensione in ingresso nel sistema: guadagno di tensione;
  • Rapporto tra la corrente in uscita e la corrente in ingresso nel sistema: guadagno di corrente;
  • Rapporto tra la tensione in uscita e la corrente in ingresso nel sistema: transresistenza;
  • Rapporto tra la corrente in uscita e la tensione in ingresso nel sistema: transconduttanza.
Dovendo effettuare l’analisi dei sistemi in frequenza, le grandezze in ingresso/uscita, ossia tensioni e correnti, sono espresse nella forma fasoriale. La funzione di trasferimento in regime delle frequenze viene indicata con i simboli H(jω) oppure G(jω).
Esiste una doppia strada per il calcolo della funzione di trasferimento: per via delle impedenze o per via delle equazioni caratteristiche.

Esempio con equazioni caratteristiche

Si vuole calcolare la funzione di trasferimento del circuito in figura 1, in particolare si vuole calcolare il rapporto tra la corrente in uscita e la corrente in ingresso.
Figura 1: circuito in analisi.

Dal circuito in figura, è possibile ricavare alcune equazioni:
dall'equazione D), essendo la corrente sul condensatore identica a quella sul resistore, si ricava un espressione per Vi, unendo con l'equazione B):
Inoltre, la tensione sul condensatore è pari alla Vi, perché il suddetto componente è posto in parallelo al generatore. Considerando l'equazione appena ottenuta e la C), si ha
Per proseguire l'analisi, è possibile trasformare questa equazione, membro a membro, tramite la trasformata di Fourier. Allo stesso modo l'equazione B)

La richiesta iniziale è quella di ottenere una funzione di trasferimento in guadagno di corrente ottenuta dal rapporto tra la corrente sul condensatore e la corrente totale del circuito. In sintesi
Tutte le componenti sono note, si può procedere a una sostituzione.
Si può sistemare l'espressione ottenuta, facendola apparire più "canonica":
l'espressione appena ottenuta è la funzione di trasferimento in regime armonico (delle frequenze) del circuito in figura 1. 

Esempio con calcolo delle impedenze

La funzione di trasferimento calcolata tramite le impedenze risulta essere più semplice. Si consideri il circuito in figura 2. Si vuole calcolare la funzione di trasferimento in guadagno di tensione ottenuta dal rapporto tra la tensione in uscita e la tensione in ingresso.
Figura 2: circuito in analisi.

Il primo step da seguire è quello di trasformare tutti i complenti in impedenze. Segue dunque il calcolo di un'impedenza complessiva. In realtà, in questo circuito è facilmente riconoscibile un partitore di tensione, in cui l'uscita viene calcolata nell'impedenza parallelo tra capacità e resistore:

La funzione di trasferimento è presto calcolata:
Basta sostituire i termini e la funzione è ottenuta.
da cui
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Una funzione di trasferimento qualsiasi può essere definita, in forma canonica, dal seguente rapporto di polinomi nella variabile jω :
Nella pratica, solitamente, il grado del polinomio a denominatore n è maggiore del grado a numeratore m. Il grado del polinomio a denominatore, inoltre, riveste una fondamentale importanza, in quanto l'ordine del sistema in esame è legato direttamente al grado del denominatore. Può dirsi che i circuiti precedentemente analizzati sono del secondo ordine, avendo il denominatore di grado massimo pari a due.
Si possono chiamare N(ω) il polinomio al numeratore e D(ω) il polinomio a denominatore. Essendo i due polinomi complessi, si definiscono:
  • zeri le radici del polinomio a numeratore;
  • poli le radici del polinomio a denominatore.
Oltre a ciò, può anche essere presente un termine costante che moltiplica tutto il rapporto. I poli e gli zeri possono avere molteplicità maggiori di uno ed essere reali, immaginari o complessi. Si può scrivere quindi una funzione di trasferimento tipica come segue: 
Tramite alcuni procedimenti algebrici, si può trascrivere la funzione di trasferimento in questo modo, nella versione a costanti di tempo:
in cui si evidenziano i seguenti componenti:

In questa rappresentazione, poli e zeri sono cambiati di segno!! Il guadagno costante ha valore 

Esempio: vuolsi rappresentare la funzione di trasferimento del secondo circuito nella forma poli-zeri.
scrivendo in una forma più "carina", otteniamo:
La prima cosa da effettuare è una soluzione del polinomio a denominatore.
Il guadagno costante K = 1 Possiamo osservare tre casi diversi, a seconda dei valori di targa dei componenti passivi.
  • delta positivo: si ottiene un discriminante positivo al denominatore se .
    Tenendo questa ipotesi, allora si può risolvere come segue
    e si ottengono due radici reali;

  • delta nullo: il discriminante ha valore zero se. Si ottiene un polo con molteplicità doppia:


  • delta negativo: il discriminante ha un valore minore di zero se, ovviamente, . 
    Si ottengono due poli complessi coniugati.
    Si raccomanda di prendere il modulo nell’argomento della radice!

Modi associati ai poli

Non appena divengono noti i poli e gli zeri, in particolare i primi, è possibile associare a ogni singolo polo una funzione definita modo. Si tratta di una funzione del tempo che mostra una sorta di anteprima di come un sistema lineare risponda a uno stimolo. In questo caso, è meglio lavorare con una funzione di trasferimento classica, non con la scrittura a costanti di tempo. I segni devono essere mantenuti
Se la funzione di trasferimento ha:
  • un polo i-esimo con molteplicità unica, il suo modo è
  • un polo i-esimo complesso e coniugato, il suo modo è

  • un polo i-esimo con una molteplicità m > 1:
I modi di un sistema saranno un utile strumento per valutare la stabilità di un sistema. Inoltre, le costanti moltiplicative saranno valutate in base alle condizioni iniziali dei circuiti. In figura 3 vi è un diagramma di Gauss dei numeri complessi che rappresenta il modo associato ai poli a seconda di dove siano localizzati nel diagramma dei numeri complessi. L'immagine è presa dalle dispense di controlli automatici del prof. Zanasi dell'UNIMORE.
Figura 3: modi associati ai poli in diversi casi del diagramma dei numeri complessi.









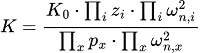
Commenti

Posta un commento

Post popolari in questo blog

Conversione analogico - digitale (ADC) e digitale - analogico (DAC) con amplificatori operazionali

-
Immagine
Convertitore Analogico - Digitale (ADC)  La conversione di un segnale da analogico a digitale (figura 1) può essere effettuata con diverse tipologie di architettura, intesa come sistema di interconnessioni tra componenti elettrici. Figura 1: schema ADC. Si supponga di avere un sensore che capti una grandezza fisica e la mandi in uscita come segnale di tensione . L'intervallo di valori di tensione che può assumere è limitato e il massimo valore si definisce fondo-scala . Il numero di bit con cui si vuole rappresentare in digitale un segnale analogico è definita risoluzion e. Conversione con risoluzione 1 bit Il caso più semplice di conversione da analogico a digitale è il convertitore a un bit di risoluzione. Il segnale analogico in ingresso può assumere qualsiasi valore tra zero e il valore di tensione di fondo-scala . Su un grafico tensione-tensione, è una semplice retta. Il margine di riferimento si ottiene dividendo a metà il valore di fondo-scala. Si effettua una quantizzazione...
Continua a leggere

Tempo di propagazione nella logica pass-transistor - legge di Elmore (39)

-
Immagine
 La logica a pass-transistor consente di realizzare porte logiche con un numero ridotto di transistori MOS. Come è stato visto per una catena di porte logiche in CMOS , si analizza ora il tempo necessario che un segnale impiega ad attraversare una catena di pass-transistors (figura 1), con le dovute approssimazioni. Figura 1: catena di pass-transistors.   Per effettuare l'analisi, in ingresso viene mandato un segnale a gradino che all'istante t = 0 passa istantaneamente da 0 a V DD . Dalla definizione di pass-transistor , l'uscita passa dal valore basso al valore alto in un dato intervallo di tempo, come mostrato nei grafici in figura 2. Figura 2: andamento della tensione d'ingresso e di uscita in una catena di pass-transistors. Il segnale alto all'ingresso e ai capi del gate di ogni transistore comporta che tra drain e source scorre una corrente che dipende dalla tensione V DS non linearmente.  Nel calcolo del tempo di propagazione, tuttavia, si farà uso di una ...
Continua a leggere

Modello di Ebers & Moll delle correnti nel BJT - Guadagni di corrente (15)

-
Immagine
 Il flusso delle correnti in un transistore bipolare a giunzione, che si tratti di un npn o pnp, è descritto dal modello di Ebers & Moll. Per il calcolo delle correnti, è necessario il modello a coppia di diodi, come mostrato in figura 1. Figura 1: circuito equivalente per bjt npn. Nel modello è stato inserito un generatore di corrente pilotato in tensione I t che rappresenta la corrente di effetto transistore. In questo contesto, i diodi sono regolati dalla legge esponenziale che lega la corrente sche scorre al loro interno con le tensioni applicate: Osservando i versi delle correnti e la legge al nodo, I E = I B + I C , si ottengono le espressioni delle correnti in funzione delle tensioni: Le tre funzioni appena ottenute sono le equazioni del modello di Ebers & Moll.   Nella realtà, solo due di queste sono di interesse: IB e IC. Essendo funzioni in due variabili, si sceglie di trattare, al fine di semplificare i calcoli, una delle due variabili come costante. I B...
Continua a leggere