Analisi della stabilità in un circuito amplificatore operazionale con retroazione negativa

-

 Analizzare la stabilità di un circuito in retrazione con amplificatore operazionale è un punto cruciale per capire come il circuito reagisce agli stimoli in ingresso. 

La stabilità di un amplificatore operazionale e del circuito di retroazione sono fortemente legati ai componenti elettronici presenti. L’analisi della stabilità viene effettuata a partire dal guadagno di anello. Il principio di Nyquist afferma che un sistema è stabile se il diagramma polare associato non tocchi e non circondi il punto critico, -1.

A questo proposito, viene di grande utilità l'analisi dei margini di guadagno e di fase, in particolar modo il secondo. Il margine di fase è la distanza angolare, nel diagramma polare, del punto che ha modulo pari a 1 dal punto critico, -1. L'obiettivo da perseguire è che il margine di fase PM sia maggiore di 45° (figura 1). La ragione di questa regola sta nel fatto che l'uscita, nel dominio nel tempo, non presenta particolare sovraelongazione, raggiungendo un buon risultato in termini di affidabilità del circuito. 

Figura 1: PM maggiore di 45°.

Secondo polo in un amplificatore operazionale

Prima di proseguire, è giusto vedere cosa accade se la f.d.t. di un amplificatore operazionale contiene un secondo polo.
si devono osservare due casi:
  1. frequenza del secondo polo maggiore della frequenza di transizione a guadagno unitario: la frequenza di transizione corrisponde ancora al prodotto GBW (guadagno - larghezza di banda) e il secondo polo non ha particolari ripercussioni sul sistema in retroazione (figura 2);
    Figura 2: secondo polo maggiore della frequenza di transizione.

  2. Frequenza del secondo polo inferiore alla frequenza di transizione a singolo polo: La frequenza di transizione non corrisponde più al prodotto GBW. (figura 3).
    Figura 3: secondo polo inferiore alla frequenza di transizione calcolata rispetto al primo (in rosa).

Per capire in quale caso ci si trova occorre prima trovare la frequenza di transizione calcolata al primo polo (a frequenza inferiore) tramite il solito calcolo. Se questa è maggiore della frequenza del secondo polo, allora ci si trova di fronte al secondo caso. Viceversa, siamo nel primo caso.

Ora, si provi a stabilire il margine di fase di un amplificatore operazionale con due poli. Il procedimento generico, anche favorito, è quello che si ottiene per via analitica, ossia eseguendo tutti i calcoli, a partire dalla frequenza di transizione del guadagno di anello e successivamente l'argomento. Si consiglia l'utilizzo dei diagrammi di bode solo con un simulatore, poiché con carta e penna si potrebbero ottenere risultati imprecisi.
Figura 4: amplificatore non invertente.

In figura 4 è raffigurato il circuito di un amplificatore operazionale invertente con una coppia di resistenze in retroazione. I dati sono i seguenti:
Per procedere al calcolo, occorre prima di tutto definire la funzione guadagno di anello tramite la coppia di funzioni di trasferimento.

Ora è necessario porre il modulo di questa funzione pari a 1 (0 dB) e trovare a quale frequenza fT ciò avviene. Per quanto concerne la f.d.t., la frequenza di transizione a singolo polo sarebbe
ma la frequenza del secondo polo è proprio la metà del valore appena trovato! La frequenza di transizione quindi non è nota. Si ponga il modulo di T pari a 1.

ora la frequenza di transizione del guadagno di anello è nota. Non ci resta che calcolare la fase a questa frequenza:
Il margine di fase risultante è

Un risultato che afferma la non completa stabilità del sistema. L'unico modo di aumentare questo margine è quello di agire sui valori della coppia di resistori. Siano dati i due resistori identici con resistenza 1 kOhm. La funzione guadagno di anello diviene:
Con lo stesso procedimento, si ricava la frequenza di transizione a guadagno unitario:

La fase del guadagno di anello alla frequenza appena ricavata è
Il margine di fase passa ora da 39° a

Il margine di fase è ora maggiore di 45°, quindi il sistema è stabile. Anche senza l'ausilio dei diagrammi di Bode, si è ricavata una stima ottima della stabilità del sistema.

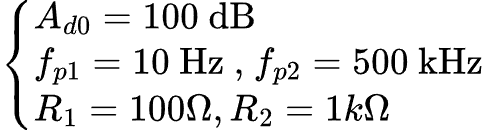
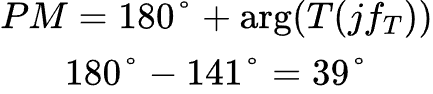
Commenti

Posta un commento

Post popolari in questo blog

Conversione analogico - digitale (ADC) e digitale - analogico (DAC) con amplificatori operazionali

-
Immagine
Convertitore Analogico - Digitale (ADC)  La conversione di un segnale da analogico a digitale (figura 1) può essere effettuata con diverse tipologie di architettura, intesa come sistema di interconnessioni tra componenti elettrici. Figura 1: schema ADC. Si supponga di avere un sensore che capti una grandezza fisica e la mandi in uscita come segnale di tensione . L'intervallo di valori di tensione che può assumere è limitato e il massimo valore si definisce fondo-scala . Il numero di bit con cui si vuole rappresentare in digitale un segnale analogico è definita risoluzion e. Conversione con risoluzione 1 bit Il caso più semplice di conversione da analogico a digitale è il convertitore a un bit di risoluzione. Il segnale analogico in ingresso può assumere qualsiasi valore tra zero e il valore di tensione di fondo-scala . Su un grafico tensione-tensione, è una semplice retta. Il margine di riferimento si ottiene dividendo a metà il valore di fondo-scala. Si effettua una quantizzazione...
Continua a leggere

Tempo di propagazione nella logica pass-transistor - legge di Elmore (39)

-
Immagine
 La logica a pass-transistor consente di realizzare porte logiche con un numero ridotto di transistori MOS. Come è stato visto per una catena di porte logiche in CMOS , si analizza ora il tempo necessario che un segnale impiega ad attraversare una catena di pass-transistors (figura 1), con le dovute approssimazioni. Figura 1: catena di pass-transistors.   Per effettuare l'analisi, in ingresso viene mandato un segnale a gradino che all'istante t = 0 passa istantaneamente da 0 a V DD . Dalla definizione di pass-transistor , l'uscita passa dal valore basso al valore alto in un dato intervallo di tempo, come mostrato nei grafici in figura 2. Figura 2: andamento della tensione d'ingresso e di uscita in una catena di pass-transistors. Il segnale alto all'ingresso e ai capi del gate di ogni transistore comporta che tra drain e source scorre una corrente che dipende dalla tensione V DS non linearmente.  Nel calcolo del tempo di propagazione, tuttavia, si farà uso di una ...
Continua a leggere

Modello di Ebers & Moll delle correnti nel BJT - Guadagni di corrente (15)

-
Immagine
 Il flusso delle correnti in un transistore bipolare a giunzione, che si tratti di un npn o pnp, è descritto dal modello di Ebers & Moll. Per il calcolo delle correnti, è necessario il modello a coppia di diodi, come mostrato in figura 1. Figura 1: circuito equivalente per bjt npn. Nel modello è stato inserito un generatore di corrente pilotato in tensione I t che rappresenta la corrente di effetto transistore. In questo contesto, i diodi sono regolati dalla legge esponenziale che lega la corrente sche scorre al loro interno con le tensioni applicate: Osservando i versi delle correnti e la legge al nodo, I E = I B + I C , si ottengono le espressioni delle correnti in funzione delle tensioni: Le tre funzioni appena ottenute sono le equazioni del modello di Ebers & Moll.   Nella realtà, solo due di queste sono di interesse: IB e IC. Essendo funzioni in due variabili, si sceglie di trattare, al fine di semplificare i calcoli, una delle due variabili come costante. I B...
Continua a leggere