Stabilità dei sistemi in retroazione - margini di guadagno e fase

-

 La stabilità è la condizione per la quale un sistema lineare risponde correttamente a un impulso in ingresso. La stabilità viene valutata sulla base del polinomio caratteristico, il denominatore della funzione di trasferimento.

Figura 1: risposte temporali all'impulso in ingresso.

Vengono definite le seguenti tipologie di stabilità :

  1. Stabilità asintotica: il sistema è asintoticamente stabile se i poli sono tutti a parte reale negativa;
  2. Stabilità indifferente: il sistema è stabile se tutti i poli sono a parte reale negativa oppure nulla. Questi ultimi devono avere molteplicità pari a uno;
  3. Instabilità: il sistema ha almeno un polo a parte reale positiva oppure un polo a parte reale nulla con molteplicità maggiore di uno.
Le tipologie di stabilità possono essere osservate nella risposta temporale dell’uscita (figura 1). Dopo aver inviato un impulso all'ingresso, se l’uscita tende verso lo zero, il sistema è stabile asintoticamente. Se, invece, l’uscita si stabilizza su un valore compreso in un preciso intervallo, allora il sistema è stabile. 

Stabilità nella retroazione

Al fine di analizzare la stabilità di un sistema in retroazione occorre prendere in considerazione diversi aspetti. In figura 2 vi e è lo schema a blocchi classico di un sistema in retroazione
Figura 2: sistema in retroazione.

la cui funzione di trasferimento è

L'equazione da risolvere, in primo luogo, per ottenere informazioni sulla stabilità è l'uguaglianza a zero del denominatore.
Risolta l'equazione, si ottengono i poli e quindi si nota subito il segno e la molteplicità.
Un altro aspetto da considerare è il prodotto tra il guadagno di ramo diretto e il guadagno di ramo in retroazione. Questo si definisce guadagno di anello ed è indicato con L. 
In secondo luogo, potrebbe essere buona pratica tracciare il diagramma di Nyquist associato al guadagno di anello del sistema in retroazione. 

L'ordine della funzione di trasferimento k viene definito sulla base dell'esponente del polo collocato in zero:

Costruire il diagramma polare di Nyquist richiede alcuni passaggi. Tuttavia, è utile prima di tutto tracciare i diagrammi di Bode associati al modulo e alla fase della funzione di trasferimento. Il diagramma di Nyquist viene tracciato sul Piano di Gauss, avente sull'asse delle ascisse la parte reale e sull'asse delle ordinate la parte immaginaria. I numeri complessi possono essere tracciati come un vettore avente una lunghezza pari al modulo e un angolo con l'asse reale pari alla fase.
 
La prima cosa da fare è calcolare i limiti della funzione di trasferimento:
e osservare la fase nel diagramma di Bode delle fasi.
La seconda cosa, poi, è osservare il modulo e la fase della f.d.t. in corrispondenza di eventuali poli e zeri, per avere alcuni punti da tracciare nel diagramma polare.

Il criterio di Nyquist sulla stabilità dei sistemi in retroazione afferma che nell'ipotesi che la funzione guadagno di anello L abbia tutti i poli a parte reale negativa oppure nulla con molteplicità singola, condizione necessaria e sufficiente per cui il sistema in retroazione è stabile è che il diagramma polare non circondi né tocchi il punto critico -1.
In figura 3 è mostrato un esempio di diagramma polare di un sistema stabile che rispetta il criterio di Nyquist.
Figura 3: diagramma di Nyquist di un sistema stabile.

Il diagramma tratteggiato in blu è una sorta di completamento del diagramma di Nyquist, sarebbe il grafico ottenuto per pulsazioni che variano da 0 a meno infinito.

Per valutare la stabilità di un sistema si è soliti quantificare i parametri margini di stabilità. 
  1. il margine di guadagno o margine di ampiezza GM è la distanza che si stabilisce tra il punto critico e il particolare punto del diagramma di Nyquist in cui la fase è pari a 180°. Il calcolo avviene in questo modo:

  2. il margine di fase PM è la distanza in gradi tra il punto critico e il punto il cui modulo è pari a uno. In formule:


La figura 4 mostra il margine di fase e il margine di ampiezza.
Figura 4: margine di fase e di ampiezza di una f.d.t. generica.

Anche Bode ha espresso un proprio criterio riguardante la stabilità dei circuiti, maggiormente utilizzato nel campo dell'elettronica: condizione sufficiente affinchè il circuito sia stabile, posto che abbia poli a parte reale negativa, è che 
invece, condizione necessaria e sufficiente per cui un sistema con soli poli negativi sia stabile è che tutti i margini di guadagno siano maggiori di uno e tutti i margini di fase siano maggiori di zero.

Nello studio dell'elettronica analogica, sarà necessario valutare correttamente il margine di fase affinché la risposta temporale in uscita dal circuito amplificatore non abbia delle oscillazioni.


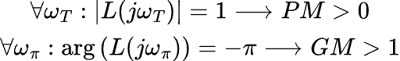
Commenti

Posta un commento

Post popolari in questo blog

Conversione analogico - digitale (ADC) e digitale - analogico (DAC) con amplificatori operazionali

-
Immagine
Convertitore Analogico - Digitale (ADC)  La conversione di un segnale da analogico a digitale (figura 1) può essere effettuata con diverse tipologie di architettura, intesa come sistema di interconnessioni tra componenti elettrici. Figura 1: schema ADC. Si supponga di avere un sensore che capti una grandezza fisica e la mandi in uscita come segnale di tensione . L'intervallo di valori di tensione che può assumere è limitato e il massimo valore si definisce fondo-scala . Il numero di bit con cui si vuole rappresentare in digitale un segnale analogico è definita risoluzion e. Conversione con risoluzione 1 bit Il caso più semplice di conversione da analogico a digitale è il convertitore a un bit di risoluzione. Il segnale analogico in ingresso può assumere qualsiasi valore tra zero e il valore di tensione di fondo-scala . Su un grafico tensione-tensione, è una semplice retta. Il margine di riferimento si ottiene dividendo a metà il valore di fondo-scala. Si effettua una quantizzazione...
Continua a leggere

Tempo di propagazione nella logica pass-transistor - legge di Elmore (39)

-
Immagine
 La logica a pass-transistor consente di realizzare porte logiche con un numero ridotto di transistori MOS. Come è stato visto per una catena di porte logiche in CMOS , si analizza ora il tempo necessario che un segnale impiega ad attraversare una catena di pass-transistors (figura 1), con le dovute approssimazioni. Figura 1: catena di pass-transistors.   Per effettuare l'analisi, in ingresso viene mandato un segnale a gradino che all'istante t = 0 passa istantaneamente da 0 a V DD . Dalla definizione di pass-transistor , l'uscita passa dal valore basso al valore alto in un dato intervallo di tempo, come mostrato nei grafici in figura 2. Figura 2: andamento della tensione d'ingresso e di uscita in una catena di pass-transistors. Il segnale alto all'ingresso e ai capi del gate di ogni transistore comporta che tra drain e source scorre una corrente che dipende dalla tensione V DS non linearmente.  Nel calcolo del tempo di propagazione, tuttavia, si farà uso di una ...
Continua a leggere

Modello di Ebers & Moll delle correnti nel BJT - Guadagni di corrente (15)

-
Immagine
 Il flusso delle correnti in un transistore bipolare a giunzione, che si tratti di un npn o pnp, è descritto dal modello di Ebers & Moll. Per il calcolo delle correnti, è necessario il modello a coppia di diodi, come mostrato in figura 1. Figura 1: circuito equivalente per bjt npn. Nel modello è stato inserito un generatore di corrente pilotato in tensione I t che rappresenta la corrente di effetto transistore. In questo contesto, i diodi sono regolati dalla legge esponenziale che lega la corrente sche scorre al loro interno con le tensioni applicate: Osservando i versi delle correnti e la legge al nodo, I E = I B + I C , si ottengono le espressioni delle correnti in funzione delle tensioni: Le tre funzioni appena ottenute sono le equazioni del modello di Ebers & Moll.   Nella realtà, solo due di queste sono di interesse: IB e IC. Essendo funzioni in due variabili, si sceglie di trattare, al fine di semplificare i calcoli, una delle due variabili come costante. I B...
Continua a leggere