Il sommatore binario, dall’ half-adder al full-adder

-

 Se in regime analogico si fa uso di un’amplificatore operazionale e alcune resistenze per eseguire la somma di segnali, in regime digitale esiste un vero e proprio blocco logico che svolge la somma di bit: il full-adder, indicato FA.

Half Adder

La somma, come nell'aritmetica decimane (studiata fin dalle elementari) prevede che due numeri sommati possano dare una somma S e un riporto C. Scelti due bit ai e bi, la somma si e il riporto ci sono ottenuti come mostrato in tabella 1:

Tabella 1: tabella della verità di somma e riporto.

Osservando la tabella, si nota dubito che la somma binaria è identicamente uguale alla funzione logica XOR (l'uscita va a 1 se soltanto uno dei due ingressi è a 1) e il riporto è identicamente uguale alla funzione logica AND. In figura 1 è mostrato lo schema logico di un Half-adder.


Figura 1: blocco half-adder.

Il difetto principale del dispositivo half-adder sta nel fatto che non viene considerato un eventuale riporto in ingresso. Con ciò significa che un eventuale sommatore a n bit non darebbe il risultato corretto. Per fronteggiare questo problema, si crea un dispositivo sommatore binario che prenda in ingresso anche il riporto dei bit precedenti.

Full-adder (FA)

Il dispositivo sommatore binario full-adder prevede lo stesso comportamento dell’half-adder, con la sola aggiunta che il terzo ingresso è destinato a prendere il riporto dei bit precedenti. In tabella 2 è mostrata la tabella di verità di somma e riporto di un full-adder.
Tabella 2: tabella di verità di somma e riporto.

La funzione riporto e la funzione somma sono così rappresentabili come espressioni logico-booleane:

In figura 2 vi è lo schema logico che rappresenta tramite blocchi AND, OR e XOR. Viste le considerazioni sui vantaggi della tecnologia CMOS, si cerca di realizzare tutte le funzioni con la suddetta logica. Nella funzione del riporto, lo XOR logico tra i bit ai e bi può essere calcolato con un OR. Questo è possibile in quanto è il risultato di una medesima mappa K, con un diverso raggruppamento.

Figura 2: schema logico del full-adder.

Il circuito logico mostra chiaramente che la composizione interna di un full-adder è fatta di una coppia di half-adder e un OR logico. Si possono fare subito due considerazioni:
  1. L’area occupata da un full-adder supera il doppio dell’area occupata da un half-adder, proprio per il fatto di avere al proprio interno due half-adder e un OR;
  2. Il tempo di propagazione valutato sul percorso critico, quello per il quale il segnale attraversa più porte logiche, è ovviamente maggiore. In un half-adder un segnale può attraversare al più una porta logica. Nel full-adder, un percorso critico potrebbe essere quello del segnale ai, che attraversa XOR1, AND2 e OR1.
Provando a progettare in CMOS il sistema, si deve partire dal concetto di logica negata, ossia le uscite di un circuito digitale CMOS sono sempre negate. La porta AND è fatta di una porta NAND (4 MOS) e una NOT (2 MOS); allo stesso modo la porta OR, costituita da un NOR (4 MOS) e un NOT (2 MOS). La porta XOR è un po' più complessa. Il procedimento di descrizione CMOS è questo:
In parole, (NOT(A) NAND B) NAND (A NAND NOT(B)). Si conclude che la porta XOR esce non negata e necessita di 3 NAND e 2 NOT. Riassumendo: 
  • 4 + 2 = 6 MOS per la porta AND. Essendoci due porte AND, si ha un totale di 12 MOS;
  • 4 + 2 = 6 MOS per la porta OR, che è singola;
  • 4 MOS per la porta NAND, presa tre volte, quindi 12 MOS, più i 4 per le porte NOT. Dunque 16 MOS per la porta XOR. Essendo presenti due XOR, si ha un totale di 32 MOS.
Sommando tutti i MOS, si ha un totale di 12 + 6 + 32 = 50 transistori MOS per costruire un full-adder.

In figura 3, vi è lo schema logico della funzione riporto, sostituendo allo XOR un OR.
Figura 3: rete CMOS del riporto.

La rete del riporto presenta 12 MOS.

Per la costruzione circuitale della rete della somma, occorre esplicitare tutta la sua espressione logica, a partire dal triplo XOR. La suddetta funzione è pari a 1 logico quando è acceso un numero dispari di ingressi. Dunque la funzione è così descrivibile:

La rete CMOS è mostrata in figura 4.
Figura 4: rete CMOS della somma.

Come prevedibile, vista la complessità dell'espressione logica e necessitando il circuito anche di tre invertitori dovuti alle negazioni dei bit a, B e del bit riporto in ingresso, la rete CMOS della somma porta con se 32 transistori MOS. 
In totale, per la somma e per il riporto sono necessari 32+12=44 transistori MOS. Una piccola riduzione della superficie occupata, rispetto al caso iniziale di 50 MOS, è avvenuta.
Una considerazione importante: in questa configurazione, la somma e il riporto vengono calcolati in modo separato l’uno dall’altro.

Valutazione dei tempi di propagazione

La valutazione del tempo di propagazione di una rete costruita in CMOS è data, in forma approssimata, dall'espressione
ed è una funzione, oltre che della capacità di carico e dell'alimentazione, anche del parametro caratteristico equivalente della rete di pull-up/pull-down.
Per capire quanto sia elevato o meno il tempo di propagazione in una rete, occorre valutare il coefficiente beta nel caso peggiore.
  • rete del riporto: il caso peggiore per la rete di pull-down si ottiene quando sono accesi in serie ai e bi, mentre è spento ci-1. Il valore del beta equivalente è:

    Per la rete di pull-up allo stesso modo il beta equivalente di caso peggiore è ottenuto quando sono accesi gli stessi MOS, con la differenza che si ha la serie di due pMOS in serie e una coppia in parallelo. Il beta equivalente è:

  • rete della somma: il pull-down porta a un caso peggiore quando sono accesi in serie ai e bi e ci-1. Essendo tre MOS in serie, il beta equivalente è: 
    Tenendo sempre accesi i tre ingressi appena definiti, la rete di pull-up vede tre pMOS in serie a un parallelo di 3 pMOS. Il beta equivalente in questo caso è:

Si conclude che, per gli schematici designati, il tempo di propagazione maggiore, sia per il riporto, sia per la somma è legato alla rete di pull-up (quando l'uscita deve andare alta).

Esiste una soluzione per fronteggiare il problema del tempo di propagazione nella rete di riporto. Essendo la CMOS una logica negata, a monte della porta NOT in figura 3 non può che non esserci in uscita la negazione della funzione riporto:
Sviluppando i calcoli interni tramite alcune modifiche, si ottiene quanto segue
e la struttura elettronica in CMOS è mostrata in figura 5.
Figura 5: rete di riporto in CMOS, seconda versione.

La particolarità di questa rete è che, rispetto alla figura 4, la posizione dei pMOS nel pull-up del caso precedente è ora assunta dagli nMOS nel pull-down. Si è verificata una sorta di scambio tra le due reti di riporto. 
Con ciò, il beta equivalente del pull-up è uguale al beta equivalente della rete di pull-down del caso precedente. Ugualmente per il pull-down. 

In virtù di queste considerazioni, è possibile asportare le due reti con beta equivalente minore, e costruire una rete di riporto con architettura speculare, in cui la posizione relativa dei transistori MOS in pull-up e pull-down è la medesima. In figura 6, è mostrata la rete speculare di riporto.
Figura 6: rete del riporto speculare.


Nessun miglioramento dal punto di vista dell'occupazione d'area, ma miglioramento del tempo di propagazione del segnale all'uscita.
Si osservi ora una possibile modifica della rete della somma, così da avere meno ingombro. L'equazione della somma in uscita dalla rete e a monte dell'invertitore è

la formula iniziale del riporto, con i procedimenti di De Morgan, diviene:
eseguendo un AND logico come mostrato nel procedimento successivo, accade:

il risultato ottenuto da questo procedimento è che la somma può essere legata al riporto. Infatti,

Il circuito è mostrato in figura 7.
Figura 7: nuova rete della somma legata al riporto.

In definitiva, la somma è stata notevolmente semplificata in virtù di una riduzione del numero di transistori. Inoltre, il riporto può entrare nella rete della somma direttamente dalla rete di riporto (negato).
Come nel caso precedente, il calcolo dei beta equivalenti.
La rete di pull-down porta a un caso peggiore quando sono accesi in serie ai e bi e ci-1. Essendo tre MOS in serie, il beta equivalente è: 
La rete di pull-up, invece, porta al caso peggiore quando sono accesi gli stessi ingressi. Tuttavia, si verifica un parallelo di tre MOS in serie al altri tre MOS. Il beta equivalente è:
Potendo procedere come per il riporto, si crea anche per la somma una struttura CMOS speculare, in cui i pMOS hanno la stessa posizione degli nMOS.
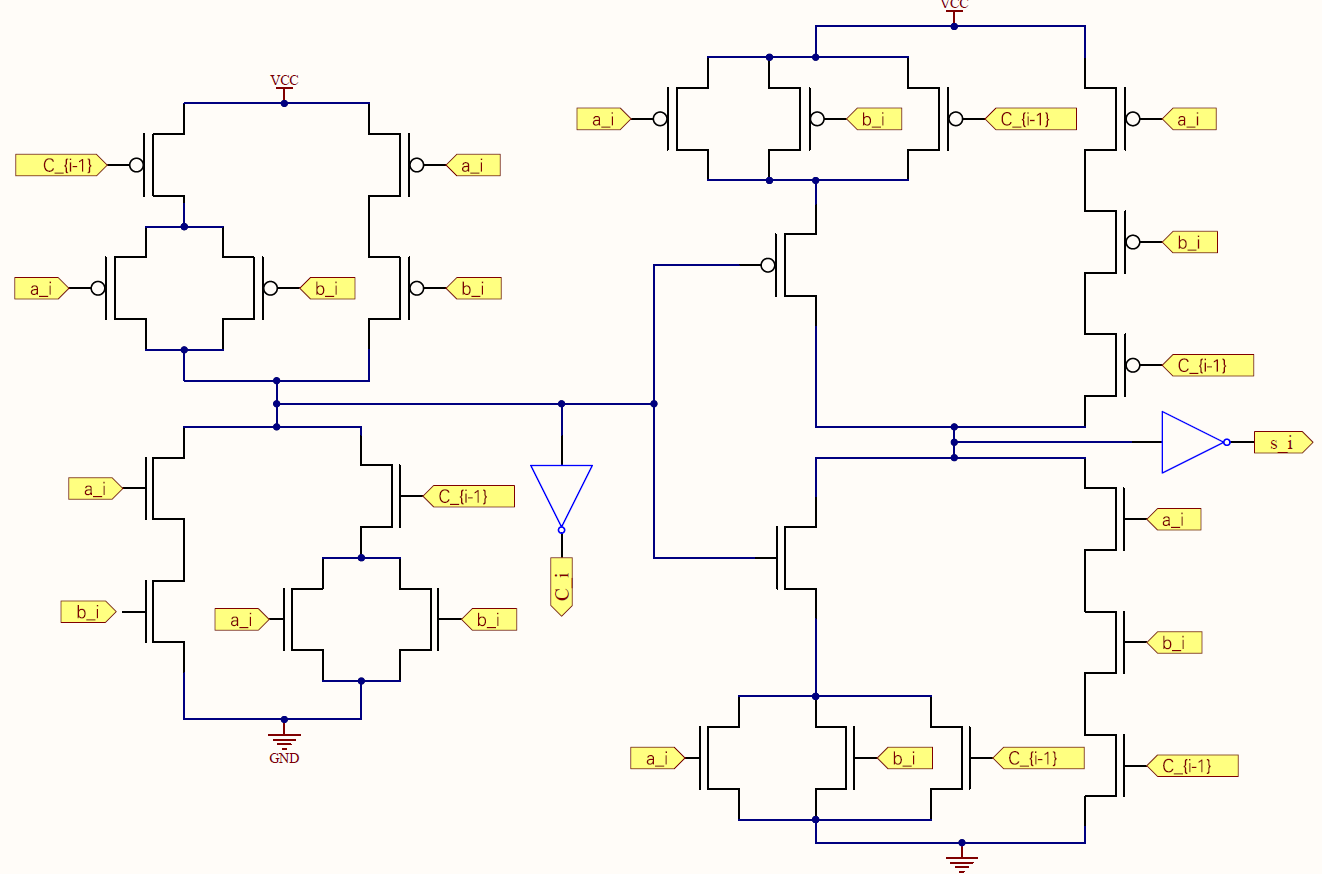In figura 8 è mostrata la struttura totale CMOS del Full-Adder Mirror.

Figura 8: Full-Adder mirror.

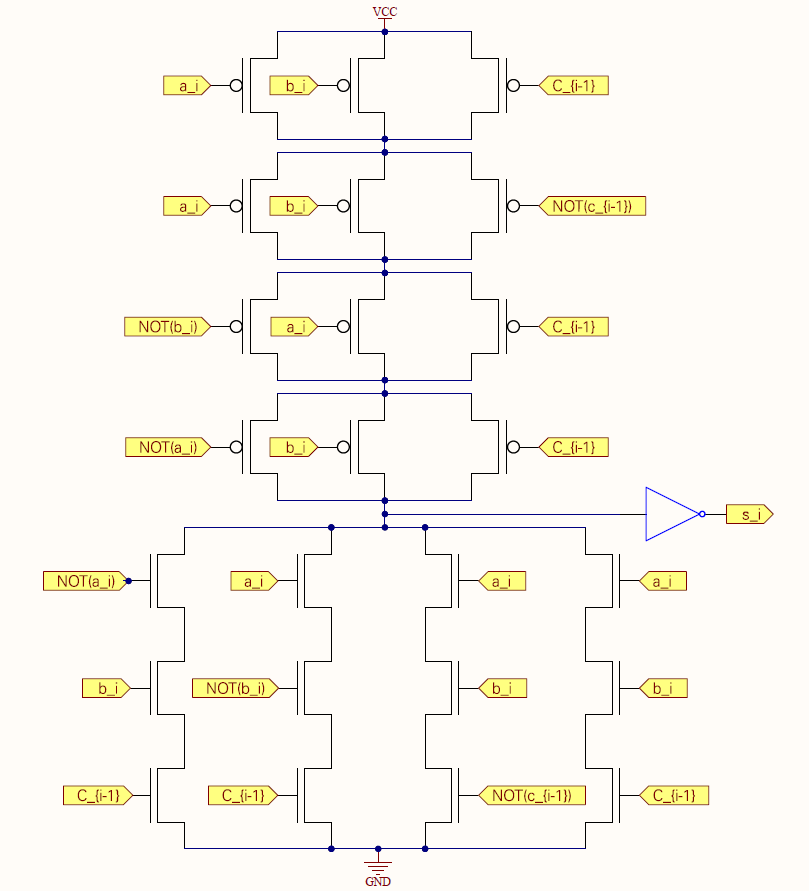
Si conclude che, sono necessari 10 MOS per il riporto, 14 MOS per la somma e 4 MOS per i due invertitori in uscita, per un totale di 28 MOS al Full-Adder.
La riduzione dell'area occupata e del tempo di propagazione dei segnali in uscita hanno avuto esito positivo. Dai 50 MOS previsti inizialmente si è arrivati a soltanto 28 MOS: in questo modo, un circuito integrato che potrà realizzare un sommatore digitale potrà contenere al proprio interno un numero consistente di full-adder.







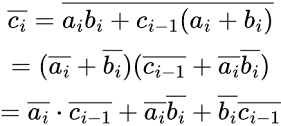
Commenti

Posta un commento

Post popolari in questo blog

Conversione analogico - digitale (ADC) e digitale - analogico (DAC) con amplificatori operazionali

-
Immagine
Convertitore Analogico - Digitale (ADC)  La conversione di un segnale da analogico a digitale (figura 1) può essere effettuata con diverse tipologie di architettura, intesa come sistema di interconnessioni tra componenti elettrici. Figura 1: schema ADC. Si supponga di avere un sensore che capti una grandezza fisica e la mandi in uscita come segnale di tensione . L'intervallo di valori di tensione che può assumere è limitato e il massimo valore si definisce fondo-scala . Il numero di bit con cui si vuole rappresentare in digitale un segnale analogico è definita risoluzion e. Conversione con risoluzione 1 bit Il caso più semplice di conversione da analogico a digitale è il convertitore a un bit di risoluzione. Il segnale analogico in ingresso può assumere qualsiasi valore tra zero e il valore di tensione di fondo-scala . Su un grafico tensione-tensione, è una semplice retta. Il margine di riferimento si ottiene dividendo a metà il valore di fondo-scala. Si effettua una quantizzazione...
Continua a leggere

Tempo di propagazione nella logica pass-transistor - legge di Elmore (39)

-
Immagine
 La logica a pass-transistor consente di realizzare porte logiche con un numero ridotto di transistori MOS. Come è stato visto per una catena di porte logiche in CMOS , si analizza ora il tempo necessario che un segnale impiega ad attraversare una catena di pass-transistors (figura 1), con le dovute approssimazioni. Figura 1: catena di pass-transistors.   Per effettuare l'analisi, in ingresso viene mandato un segnale a gradino che all'istante t = 0 passa istantaneamente da 0 a V DD . Dalla definizione di pass-transistor , l'uscita passa dal valore basso al valore alto in un dato intervallo di tempo, come mostrato nei grafici in figura 2. Figura 2: andamento della tensione d'ingresso e di uscita in una catena di pass-transistors. Il segnale alto all'ingresso e ai capi del gate di ogni transistore comporta che tra drain e source scorre una corrente che dipende dalla tensione V DS non linearmente.  Nel calcolo del tempo di propagazione, tuttavia, si farà uso di una ...
Continua a leggere

Modello di Ebers & Moll delle correnti nel BJT - Guadagni di corrente (15)

-
Immagine
 Il flusso delle correnti in un transistore bipolare a giunzione, che si tratti di un npn o pnp, è descritto dal modello di Ebers & Moll. Per il calcolo delle correnti, è necessario il modello a coppia di diodi, come mostrato in figura 1. Figura 1: circuito equivalente per bjt npn. Nel modello è stato inserito un generatore di corrente pilotato in tensione I t che rappresenta la corrente di effetto transistore. In questo contesto, i diodi sono regolati dalla legge esponenziale che lega la corrente sche scorre al loro interno con le tensioni applicate: Osservando i versi delle correnti e la legge al nodo, I E = I B + I C , si ottengono le espressioni delle correnti in funzione delle tensioni: Le tre funzioni appena ottenute sono le equazioni del modello di Ebers & Moll.   Nella realtà, solo due di queste sono di interesse: IB e IC. Essendo funzioni in due variabili, si sceglie di trattare, al fine di semplificare i calcoli, una delle due variabili come costante. I B...
Continua a leggere