Tempo di propagazione nella logica pass-transistor - legge di Elmore (39)

 La logica a pass-transistor consente di realizzare porte logiche con un numero ridotto di transistori MOS. Come è stato visto per una catena di porte logiche in CMOS, si analizza ora il tempo necessario che un segnale impiega ad attraversare una catena di pass-transistors (figura 1), con le dovute approssimazioni.

Figura 1: catena di pass-transistors.

  Per effettuare l'analisi, in ingresso viene mandato un segnale a gradino che all'istante t = 0 passa istantaneamente da 0 a VDD. Dalla definizione di pass-transistor, l'uscita passa dal valore basso al valore alto in un dato intervallo di tempo, come mostrato nei grafici in figura 2.

Figura 2: andamento della tensione d'ingresso e di uscita in una catena di pass-transistors.

Il segnale alto all'ingresso e ai capi del gate di ogni transistore comporta che tra drain e source scorre una corrente che dipende dalla tensione VDS non linearmente. 
Nel calcolo del tempo di propagazione, tuttavia, si farà uso di una approssimazione lineare della corrente che scorre tra drain e source di ogni stadio pass-transistor. Si sostituisce il transistore MOS con una resistenza (figura 3). Tutte le resistenze e le capacità sono identiche, essendo i transistori tutti uguali.

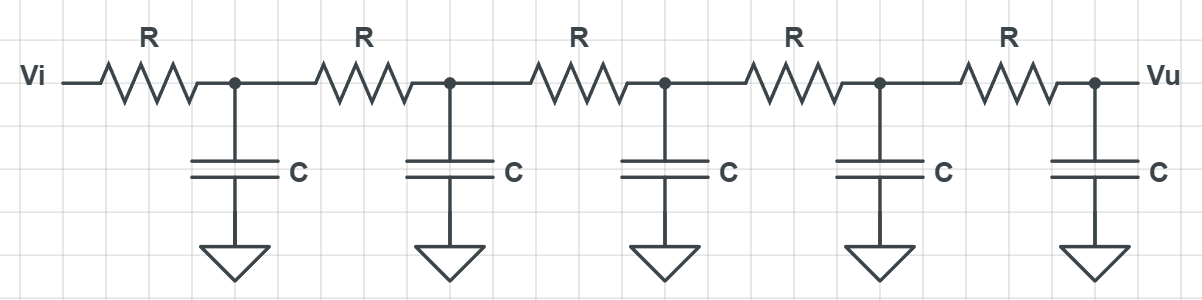Figura 3: catena di pass-transistor approssimata con resistenze.

La catena è diventata ora una cascata di filtri RC del primo ordine. In questo contesto, tuttavia, si omette la parola filtro, in quando non stiamo elaborando alcun segnale particolare in cui sia di interesse la frequenza.

• Singolo stadio (figura 4): semplicissimo circuito RC serie, la corrente della resistenza eguaglia la corrente sul condensatore.

  

  figura 4: RC serie - uno stadio pass-transistor

  
  La tensione V1 è l'ingresso, che passa da 0 a VDD nell'istante t = 0. L'espressione dell'uscita si ottiene come:
  
  e dall'espressione dell'uscita stessa si può ottenere il tempo di propagazione del singolo stadio pass-transistor
  
  
  
• Doppio stadio (figura 5): cascata di due circuiti RC serie

  

  Figura 5: doppio circuito RC serie - due stadi pass-transistors.

  
  nel caso precedente è stata ricavata un'espressione lineare per V1. Essendo la resistenza dell'ultimo stadio in serie con l'ultima capacità, è possibile affermare che la corrente che scorre sulla prima resistenza a destra è la somme delle correnti sulle capacità.
  
  nel calcolo, essendo il procedimento una approssimazione lineare, scompaiono le derivate di ordine maggiore al primo.
  
  
  Posto che V2, essendo il segnale di ingresso di questa catena, vada da 0 a VDD nell'instante t = 0, la tensione di uscita avrà espressione
  
  avvalendoci dello stesso procedimento per il calcolo del tempo di propagazione, ossia il tempo necessario a raggiungere metà della tensione di alimentazione, si ottiene:
  
  il tempo del doppio stadio è cresciuto di tre volte rispetto al singolo stadio;
  
  
• Triplo stadio (figura 6):

  

  Figura 6: cascata di tre RC serie - 3 stadi pass-transistors.

  
  in questo caso, la corrente sulla prima resistenza è data dalla somma delle correnti sulle tre capacità. Le espressioni di V1 e V2 sono note dai casi precedenti.
  
  eliminando tutte le derivate di ordine superiore a uno ed effettuando tutti i calcoli, si ottiene:
  
  Poiché si procederebbe allo stesso modo dei casi precedenti, per intuito il tempo di propagazione è legato al coefficiente della derivata della tensione di uscita. Il risultato che si ottiene è il seguente:
  
  che è due volte maggiore del doppio stadio e sei volte maggiore del singolo stadio pass-transistor.

I calcoli appena eseguiti portano al risultato ricercato, infatti, come mostra la tabella,

Osservando i coefficienti numerici del tempo di propagazione, si può notare che cresce con una successione aritmetica:

• 1 = 1;
• 3 = 1 + 2;
• 6 = 1 + 2 + 3;
• 10 = 1 + 2 + 3 + 4;

Il coefficiente che moltiplica RC ln(2) risulta essere la somma di tutti gli n numeri naturali. La somma di n numeri è data dall'espressione

Alla fine, il tempo di propagazione di una catena di n pass-transistors è dato dalla seguente equazione:

il risultato è chiaro, ossia il tempo cresce con il quadrato del numero di stadi a pass-transistor presenti. Questa formula è anche detta legge di Elmore del ritardo.

La logica CMOS, invece, ha dato una crescita del tempo di propagazione lineare con il numero di stadi.

Tuttavia, non si può dire che la logica CMOS sia sempre migliore della logica a pass-transistor. Può esistere un valore specifico di n, come mostrato nel grafico in figura 7, per cui valori inferiori a esso presentino un tempo di propagazione inferiore per la logica a pass-transistor rispetto alla logica CMOS.

Figura 7: andamento del tempo di propagazione nella logica CMOS (verde) e pass-transistor (rosso).