Tempi di propagazione in una catena di porte logiche CMOS (36)
 |
| Figura 1: catena di invertitori CMOS. |
a parte la mobilità, che di norma non può essere modificata, se non con procedimenti di drogaggio, può decidersi, a livello circuitale, di aumentare l'alimentazione nei limiti del buon funzionamento. Inoltre, a livello di processo tecnologico, può essere ridotta la lunghezza del canale fino al limite imposto dalle ultime tecnologie appunto.
La figura 1 rappresenta una catena di invertitori CMOS, che modellizzano una sequenza di porte logiche, ridotte a un semplice invertitore con il classico procedimento di MOS in serie e in parallelo.
Dimensionamento singolo stadio
Tutti gli invertitori sono caratterizzati dallo stesso coefficiente β, definito β0, quindi tutti i transistori hanno le stesse dimensioni geometriche. Per semplicità, avranno tutti larghezza di canale W0 e Lmin. Note queste informazioni, si può affermare che il tempo di propagazione di tutti gli invertitori sarà identico, eccetto per l'ultimo, che è seguito da una capacità CL molto più grande delle capacità C0.
Come già affermato, la capacità di carico CL è molto maggiore della capacità associata agli invertitori C0, si supponga di un fattore N >> 1. Il tempo di propagazione dell'ultimo stadio invertitore è N volte maggiore del tempo appena calcolato:
 |
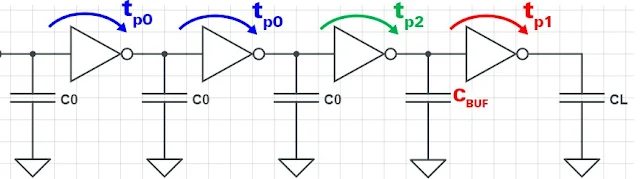
| Figura 2: tempi di propagazione buffer. |
Questa è la tipica situazione che si verifica quando si interfaccia un circuito integrato con l'esterno (chip su PCB ad esempio).
Si rende necessario dimensionare l'ultimo stadio, definito buffer (figura 2). Poiché non è possibile toccare la capacità di carico, si prova a modificare il parametro geometrico larghezza W0, direttamente proporzionale al coefficiente β. Si vuole quindi una larghezza WBUF che sia k volte maggiore della larghezza iniziale:
Il tempo di propagazione del buffer risente giustamente del dimensionamento
Il fatto contrario di questo dimensionamento è l'area occupata: aumentare la larghezza di un transistor significa occupare più superficie sul chip.
Inoltre, la capacità che precede lo stadio di buffer risente del dimensionamento. Chiamandola CBUF, si può osservare facilmente che cresce del fattore k e allo stesso modo il tempo di propagazione dello stadio invertitore precedente il buffer:Poiché non viene toccato dimensionalmente il suddetto stadio, il coefficiente β rimane tale β0
 |
| Figura 3: situazione finale buffer. |
il tempo di propagazione a valle degli ultimi stadi invertitori è la somma dei due contributi:L'unico parametro su cui si può agire è il fattore k. Derivando l'espressione appena ottenuta rispetto a k ed eguagliando a zero, si ottiene valore di k tale da minimizzare il tempo di propagazione del segnale attraverso gli ultimi due stadi
Dimensionamento graduale
Si consideri, come nel caso precedente, una catena di n invertitori CMOS in cascata (figura 4). Questa volta, si verifica che:
- tutti i transistori hanno dimensioni geometriche diverse, il più piccolo ha coefficiente β0;
- le capacità associate crescono anch'esse con l'aumentare delle dimensioni.
 |
| Figura 4: invertitori CMOS in cascata (seconda versione). |
Poiché i coefficienti β crescono, per ipotesi i tempi di propagazione devono diminuire andando avanti con gli stadi invertitori:
Le capacità, tuttavia, sono in rapporto tra di loro secondo una sorta di regola della catena. Il rapporto di ogni capacità con la precedente è pari a un fattore k.
cade l'ipotesi della diminuzione del tempo di propagazione si sceglie di avere il primo e secondo stadio caratterizzati dallo stesso coefficiente β. Tutti gli stadi dopo il secondo hanno il medesimo tempo di propagazione ed è legato al fattore k.
vista la presenza di n stadi, il tempo di propagazione totale èInoltre, dal caso precedente considero ancora valida la dimensione della capacità di carico, più grande N volte della capacità iniziale C0il rapporto qui rappresentato deve riferirsi direttamente al fatto che tutte le capacità sono tra di loro in rapporto l'una con la precedente. Si può dunque scrivere:Il prodotto che compare in questa espressione è ben noto, poiché compaiono tutti i rapporti tra le capacità; rapporti dei quali si conosce il valore, k. Si può concludere che:si arriva a ottenere un sistema di due equazioni in due incognite, che sarà utile al calcolo del tempo di propagazione totale
Ancora una volta deve essere effettuata la derivata dell'espressione appena ottenuta, in modo da ottenere il valore di k tale da minimizzare il tempo di propagazione totale.
In conclusione, il valore che minimizza il tempo di propagazione è proprio uguale al numero di Eulero, e, approssimabile solo con 2,718. Il dimensionamento è concluso.
Come nel caso precedente, il contro di questo processo è l'occupazione d'area all'interno del chip che ospita la catena di porte logiche.

.png)
.png)
.png)

.png)
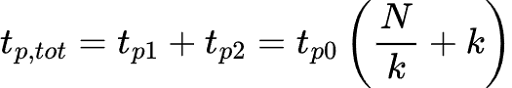
.png)
.png)
.png)
.png)
.png)
.png)
.png)




Commenti
Posta un commento